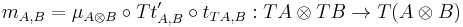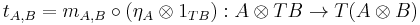Strong monad

In category theory, a strong monad over a monoidal category 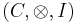$(C,\otimes,I)$ is a monad 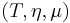$(T,\eta,\mu)$ together with a natural transformation 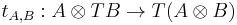$t_{A,B}�: A\otimes TB\to T(A\otimes B)$ , called (tensorial) strength, such that the diagrams

, ,

and

commute for every object $A$ , $B$ and $C$ .

Commutative strong monads

For every strong monad T on a symmetric monoidal category, a costrength natural transformation can be defined by

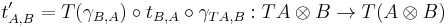$t'_{A,B}=T(\gamma_{B,A})\circ t_{B,A}\circ\gamma_{TA,B}�: TA\otimes B\to T(A\otimes B)$ .

A strong monad T is said to be commutative when the diagram

commutes for all objects $A$ and $B$ .

One interesting fact about commutative strong monads is that they are "the same as" symmetric monoidal monads. More explicitly,

a commutative strong monad 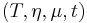$(T,\eta,\mu,t)$ defines a symmetric monoidal monad 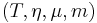$(T,\eta,\mu,m)$ by

$m_{A,B}=\mu_{A\otimes B}\circ Tt'_{A,B}\circ t_{TA,B}:TA\otimes TB\to T(A\otimes B)$

and conversely a symmetric monoidal monad 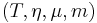$(T,\eta,\mu,m)$ defines a commutative strong monad 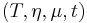$(T,\eta,\mu,t)$ by

$t_{A,B}=m_{A,B}\circ(\eta_A\otimes 1_{TB}):A\otimes TB\to T(A\otimes B)$

and the conversion between one and the other presentation is bijective.

References

Anders Kock (1972). "Strong functors and monoidal monads". Archiv der Math. 23: 113–120. doi:10.1007/BF01304852. http://home.imf.au.dk/kock/SFMM.pdf.
Eugenio Moggi (1991). "Notions of computation and monads". Information and Computation 93 (1). http://www.disi.unige.it/person/MoggiE/ftp/ic91.pdf.
Jean Goubault-Larrecq, Slawomir Lasota and David Nowak (2005). "Logical Relations for Monadic Types". Mathematical Structures in Computer Science 18 (06): 1169. arXiv:cs/0511006. doi:10.1017/S0960129508007172.